
Have you ever heard how a CNC milling machine or a 3D printer plays music? If so, then it has most likely been a Cartesian coordinate device or even a DeltaBot, but only monophone. Because producing polyphonic music using a DeltaBot is much more complicated and requires more computation than Cartesian coordinates. How it works in principle, you will learn here.
Table of contents
General information
The most people who are reading this article have probably seen one or more videos of CNC milling machines playing music. How this works in principle, I have already described here. These machines normally have an Cartesian drive, that means one motor moves the cutter along a Cartesian coordinate (along one dimension). This construction is perfect for creating music because the speed of the spindle along a coordinate is directly proportional to the rotational speed of the respective motor and so it is also directly proportional to the frequency at which the motor is energized. In other words: if I want to create twice the frequency with one motor, then I tell the milling program twice the velocity along the coordinate axis. As all common milling and 3D printing programs work with Cartesian coordinates, you can relatively (!) easily create the G-code from a MIDI file (e.g. with my Music → G-code converter). At least relatively easily compared to a so-called DeltaBot.
DeltaBot
Construction
I think there are no milling machines in DeltaBot design because this construction is not appropriate for high forces. However, there are some 3D printers with this design. Furthermore, here I should mention that there are different DeltaBot designs. I will concentrate on this DeltaBot:
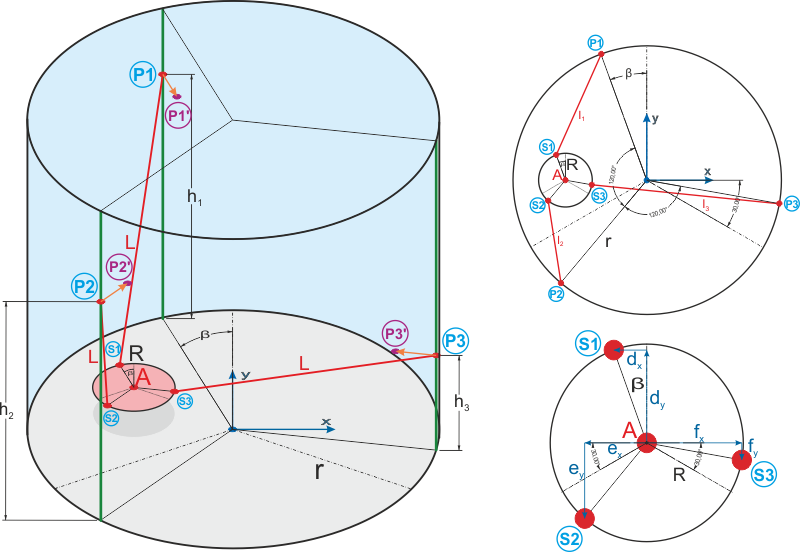
Principle
This DeltaBot basically works as follows: a total of three motors move the points P1, P2 and P3 along the green lines. Depending on the position of these three points, the position of the point A changes because the red disk is connected by three rods with the points P1, P2 and P3.
Create music with a DeltaBot
I always continue to develop my MIDI → G-code converter, and so I thought a few weeks ago, with such a DeltaBot you could also create music (as with CNC milling machines). In principle, that really works but in Reality it is computational relatively expensive and complex! First of all, you should think about, what you have to tell the milling- or 3D-printing program in principle: you have to tell the program the coordinates and speed of point A. And there is the big problem. It is useless to me, if I define the position and speed of the point A, as this point does not generate sounds or music. The sound is generated by the three motors which move the points P1, P2 and P3. To create music so you have to be able to define the positions and velocities of the points P1, P2 and P3 and calculate with these data the velocity and position of the point A. The inverse direction you should also be able to calculate, so that you know in which area the points P1, P2 and P3 can move.
Forward and reverse kinematics calculations: result
Since all the formulas of the calculation of both the forward kinematics and the reverse kinematics are relatively unattractive, I do not want to present the results on this page for the sake of clarity. If you are familiar with higher mathematics and are more interested in it, you will find all the calculations in this PDF [German].Conclusion
In case you had a look at the PDF, you can say that the music generation (the calculation of the G-Code) with a DeltaBot is a lot more difficult and computationally expensive. This article creates the theoretical basis for the implementation of a music → G-code converter for DeltaBots. I hope that my calculations are correct and that I have not forgotten or ignored any fundamental aspects. Of course, I try to expand my Music → G-code converter with this calculation rules but it will probably take some time. In particular, I also hope that this is not too computationally expensive, because the complete calculation must be done for each G-code line.




